Unlock the Ancient Power: Exploring Vedic Geometry Through 4 Timeless Areas | Revealing 5 Geometrical Wonders and Secrets

Introduction

Temples are the heart and soul of Indian culture and heritage, and they stood the test of time since thousands of years. The grandeur of the sculptures on these temples, its architecture, the way they are built, thousands of years ago, just unparalleled.

Well, it’s very difficult to just draw a perfect circle with a free hand. What could have been the geometrical expertise of people back then who built these grand structures?

That was the question we had, and this post is a result of our attempt to understand what the Vedic geometrical expertise of ancient Indians has been. To set the context, geometry is a very natural thing.

Almost all the civilizations express their culture and heritage in some form or shape in which geometry takes the center stage.

Sources of Vedic Geometry

This Post is purely to understand from an ancient Indian standpoint what was their expertise with respect to geometry back then. For ease of expression, we picked up the word Vedic geometry as broadly to encompass geometry as described in all the ancient Indian scriptures.

So the first place where we find the Vedic geometry applications is in Kalpa. It deals with executing the Vedic rules. It deals with the Vedic rituals of Yagnyam for different purposes.

The second place where we find geometry is in Jyotisha. It deals with astronomical studies that’s essential for a Vedic culture. Moving next, in the third place where we find geometry is in Shilpa Shastra, a branch of knowledge that deals with the temple construction and sculpting.

The fourth and the last area where we find geometry is in Srividya. It is a specialized branch of divine worship which is broadly categorized as Tantra. But for ease of expression, we’ll use the word Srividya.

It deals with construction of complex, two-dimensional and symmetrical geometrical diagrams that are the manifestations of different gods. And this blog post is about how geometry thrived in these four areas since times immemorial. Let’s briefly flip over these four starting with Shilpa Shastra.

Shilpa Shastra is a very broad term which is generally used for categorizing all the scriptures that deal with the temple construction, sculpting, metallurgy, architecture and a lot more.

There are many scriptures under Shilpa Shastra like Maanasara, Vastu Shastram, Shilpa Ratna kosa and many more. All the geometrical principles that are needed for temple construction are explained in these scriptures.

Up next is Jyotishya. This is one of the most misunderstood branches of knowledge that it’s about future prediction etc etc. But Jyotishya, the word literally means study of light. It deals with computation of planetary positions and as part of it, there are a lot of geometrical principles that are detailed out in the scriptures. We’ll see them as well in this post.

In India, when it comes to divine manifestation, gods are always depicted in forms of sculptures or murtis. And that’s what we generally see in the temples. But there is another practice where the divine incarnations of gods are manifested in the form of a two-dimensional symmetrical diagrams.

So Srividya details about construction of these complex geometrical figures which deals with different geometrical shapes and the principles behind their construction.

The fourth one is Kalpa. Kalpa deals with setting the guidelines for execution of the Vedic rituals like Yagnyam. And you might have seen the fire altar which is typically in a square shape like it’s shown here.

But there are a lot many other shapes which needs to be constructed depending upon the intent of the ritual. So because of that, there are a lot of geometrical concepts detailed out in Kalpa as well.

Now let’s see each of these four in detail starting with the first one, Kalpa. How the Vedic geometry is defined in Kalpa.

So Kalpa is the code of Yagnyam. It has all the rules and regulations and bylaws related to how you execute a Vedic ritual. And it has two parts to it. The first one is Sulbha Sutras.

This talks about the rules of the logistics that are needed for an Yagnyam. As to how you construct these fire altars, the Yagnya Shala and a lot more.

And the second one is Shravata Sutras which contain the mantras and the Vedic hymns which are needed for execution of the ritual.

So Sulbha Sutra is about preparation and Srauta Sutra is about execution. And you will get to know in a minute why we are talking about these.

Now Sulbha Sutras, it’s two words. Sulbha and Sutras. Sulbha means rope and Sutras means principles. So basically these are the mathematical instructions that are crucial in construction of the fire altars in the process of Yagnyam.

So thousands of years ago, they did not have scales like what we have now. So a rope is used as an instrument to measure any surface. And hence with that name goes Sulbha Sutras. In simple words, these are the geometrical principles.

The concept of Yagnyam is a very very ancient practice which has been thriving in India since no one knows when. You take any kind of ancient Indian scripture, you will not find it without reference to some kind of Yagnyam. Such is the antiquity of this ritual.

So what you are seeing on the above picture is a relic of one of such. As part of one of these rituals, there are three fire altars that should be maintained in every household back then. It is called as Treta Agni or in simple words, three fire altars. They are Ahavaniya, Grahapatiya and Dakshaniya. As you are seeing in the markings.

As you see the shapes, they are circle, square and semi-circle. The most important aspect here is there is a very strong constraint which says that all these three fire altars should have exactly the same area.

Now I don’t know what is the religious significance behind that constraint. But all these three if constructed at a place should be exactly of the same area.

This might not sound as a big deal to you now because we have all the formulas invented for calculating the areas of these shapes. But thousands of years ago, geometry was totally in a different format. So how did the ancient Indian Rishis manage to measure areas of these kinds of fire altars thousands of years ago? Now let’s see.

Basic Vedic Unit of Measurement – ANGULA

Talking of measurement, the first thing is unit of measurement. So what was the unit of measurement back then? It is Angula. This is the basic unit of measurement as per Sulbha Sutras. 34 sesame seeds stacked up against each other in a line. That is the length of a book. That is the length of one Angula.

That was basically the unit of measurement of people back then. So that comes around 4 to 5 inches as per our inches today. Also sesame seeds are one of the oldest known sources of oil to humanity. So that also explains the antiquity of the Vedic rituals and the time they belong to.

Let’s take a very simple problem to understand how the ancient Indian people constructed these fire altars. Can you draw a square with its sides perfectly aligned with the four cardinal directions?

You will need definitely a pencil, compass, paper and a scale. Without these we cannot draw a square with its sides perfectly aligned with the four cardinal directions. It’s a simple thing, right? But back then none of these were available. No compass, pencils or scales. So how did they go about it?

Let us see. So first things first. Identifying the four cardinal directions. These are not fixed because of the solstice. The sun movement varies from season to season, right?

So we need to get the directions which are applicable on that day of the execution of this ritual. So here is how they did. They took a long stick and erected on a plain ground. And then tie a string to the stick and the other end of the string tie to a nail. And then draw a circle around the stick like this. And this has to be done before the sunrise. And once sun rises, the shadow of this stick is casted on the opposite direction.

So the longest shadow will be in the early morning. So the shadow protrudes out of the circle that was drawn. And as the sun progresses over the day, proportionally the shadow reduces. And in the evening, again it protrudes towards the sun. And the sun rises towards the other end.

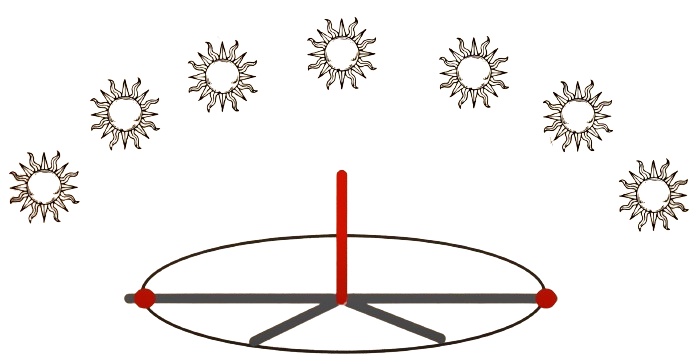
So these two spots which cross over this circular path.These two points give the east-west line.

Construction of Square with Sulbha Sutras

Once you have the east-west line, the next step is to construct a square. Take the east-west line and draw it to the length of the square you want, for example, 10 angulas.

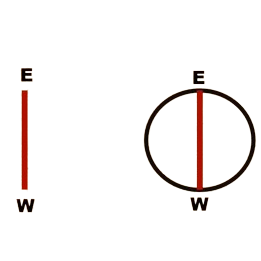
Use the east-west line as the diameter to draw a circle. Measure 10 angulas with a rope and use the east-west line as the diameter to draw a circle around it. Then, with the same diameter, draw a circle around E as the center. Next, take a point on the circle that is perpendicular to the east-west line.

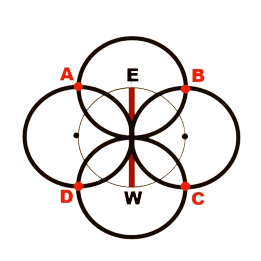
Draw a circle around that point with the same diameter as the east-west line. Repeat this process with W as the center and the opposite point. This will give you four circles.

The intersection points of these four circles (A, B, C, D) need to be plotted.

Joining A, B, C, D will give you a perfect square with its sides aligned with the four cardinal directions and the desired length, which in this case is 10 angulas.

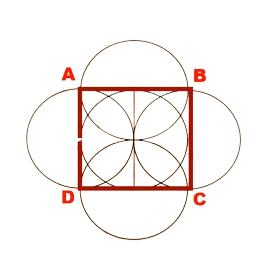
So this is how geometry was back then. Very primitive but still precise as well. So once you construct the square on the ground, that forms as the marking for construction of the square-shaped fire altar, or the Yajna Kundam.

So coming back to Treta Agni where we started, we now have the markings needed for construction of a square-shaped fire altar, as you can see in above picture. Now they have to construct a circular one which has exactly the same area as the square. So how is that possible? Let’s see.

We cannot talk the geometry of a circle without pi. But back then, the pi was not discovered yet. The credit of pi goes to Greeks or arguably Egyptians, one of these two civilizations. Indians don’t know about pi during those times. Remember, we are talking about couple of thousands of years ago. Don’t just go with current datings of 500 BC or 1000 BC. It is much much older than that.

So back then, pi was not discovered yet. So here is a beautiful postulate given by Sulbha Sutra on how to convert square, which we already have, to transform that into a circle of exactly the same area. And here is the process given in Sulbha Sutras.

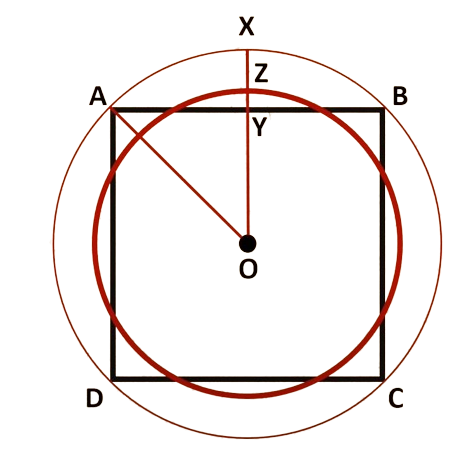
Draw a circle A, B, C, D. And then mark X and Y extending O. So you have X and Y. As part of X and Y, divide it into three parts. So that mark Z as one-third of XY. So YZ is one-third and ZX is two-thirds of XY.

And finally, draw a circle with OZ as the radius. So this is the most important thing. With OZ as the radius, the circle that you are drawing here is exactly of the same area as the square ABCD.

So this was a postulate that was given, which can be geometrically proved today as well. If you want, try it out. It’s really great to see how organically geometry has evolved over the times.

So we just saw the process of how we construct the circular fire altar as well, which is exactly of the same area as the square. Like this, there are many many geometrical principles explained in Sulbha Sutras.

But for now, let’s move on. These fire altars are called as Chiti in Sanskrit. And depending on the intent of the Yagnyam, the shape of the Chiti varies.

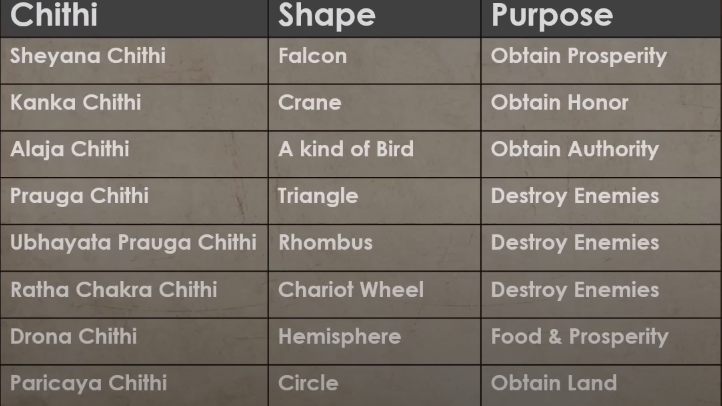
For instance, to obtain prosperity, a falcon-shaped Chiti is constructed. To destroy the enemies in war, a triangular or rhombus kind of a Chiti is constructed. And to pray for food and prosperity of the kingdom, a hemisphere shape of Chiti is constructed.

So it depends on the intent. The process given for the Yajnam is different and so is the shape of the Chiti. This is very important because this has defined the dynamics of Vedic geometry.

Shapes of Yagnya Chithis

So these Chitis are not just made out of mud. They are made out of brick arrangements. And this is how the blueprints of couple of Chitis like Shena Chiti, Radha Chakra Chiti and Kurma Chiti are.

So this is from Kalpa which ascribes to Yasur Vedam. So here the most important aspect is the bricks need to be baked according to the dimensions given here. And that needs to fit exactly in the shape of the Chiti. If you observe the shapes of the bricks, they are squares, rectangles, triangles, rhombus, trapezium. So here is where the Vedic geometry gets totally into another level.

Here is an example of Shena Chiti which shows a miniature model about how the bricks needs to be cut. Observe the tiles how they are shaped.

They are right angle triangles, isosceles triangles, squares, rectangles, everything stacked up to form the shape of a Garuda or a Falcon. Which is an exact replica of the blueprint that you are seeing here down below. And all the wooden equipments that you are seeing around it are the ones that are needed for executing a Yagnyam.

The interesting part here is, what is the geometry behind cutting and baking of these bricks? That gives us some incredible facts about Vedic geometry. Let’s see what they are.

To calculate the dimensions of these bricks based on the shapes, there are a lot of formulas or principles given in Sulvasutras.

Here I just picked up one example which is very relevant to you and me based on what we learned in our school. This is how it reads.

दीर्घचतुरश्रस्याक्ष्णया रज्जुः पार्श्वमानी तिर्यग् मानी च यत् पृथग् भूते कुरुतस्तदुभयं करोति ॥

Basically it talks about a rectangle. But let’s break it down word by word to understand the exact meaning of it.

Maharishi Baudhayana Sulbha Sutram

So basically what it says is, the area made by the horizontal and the vertical lines of a rectangle is equal to the area made by the diagonal. This is called as Pythagoras theorem in today’s world. But is actually written by Maharshi Baudhayana who is conservatively dated as 800 BC. But again, like I said, how old is Yagnyam? That old is this Kalpa. So you cannot frankly date how old are these scriptures.

So a safe and a fair statement would be, as old as Yajurvedam, so old is this principle given by Maharshi Baudhayana which is commonly called as Pythagoras theorem today.

Application of Maharishi Baudhayana Sulba Sutra

Take a look at above picture. This is Shainachiti which is in the form of a Garuda or a Falcon. Look at the size and the shape of the bricks. They are in triangular forms, stacked up into five layers.

Now the geometry behind cutting and baking of this brick, is fully based on Sulbha Sutras, even today. And the so-called Pythagoras theorem which you just saw, is just one of the many geometrical principles given by Maharshi Baudhayana.

If you observe it from this direction, you can see clearly how the entire fire altar is in the shape of a Falcon, like we have seen in the blueprint. So on top of this, the entire Yagnyam will be performed.

Now because of these five layers, the complexity behind the geometrical construction of these bricks even gets multiplied. It takes to a level of three. It will even above. Let’s see what it is.

Let’s take the isometric view of the blueprint of Shainachiti. Here if you see, it has five layers, all exactly in the same shape. And there is an additional constraint that is imposed by the Sulbha Sutras, that there should be only five layers in this one. And each layer can have only two hundred bricks. And in five layers, so that is one thousand bricks.

So you have to finish this entire construction of Shainachiti, in just one thousand bricks, with exactly two hundred bricks per layer. And if you are thinking that it is complex, it is still not done yet.

Sheyana Chithi Per Layer 200 Bricks, total 5 layers of 1000 Bricks

The five layers of the Shainachiti, the layout for one, three and five, the odd numbers layout is different from that of the even numbers. So towards left what you are seeing here is the layout for the odd numbers, and the right side is for the even numbers.

So two hundred bricks, two layouts, five layers, no scale, no equipment, nothing. In a very primitive way, the entire geometry has been executed. And this is just an example to show how complex process is, the problems Sulba Sutras dealt with.

This is the reason why Sulba Sutras are considered as world’s oldest applied geometry. And after Sulba Sutras, we have the Euclidean geometry that came in 300 BCE. Ninety-nine percent of Indians today are not aware of Sulba Sutras. Just for one reason, we don’t care about our own history and heritage.

Talking of history, here is a bit more about the Pythagoras theorem. The Pythagoras theorem or the Pythagoras triplets which satisfy the Pythagoras theorem, first found in Babylon, which is modern-day Iraq, inscripted on a stone tablet called as Plimpton 322.

That’s the code name given to the tablet. But it is dated to 1800 BCE, which is first found in Babylon. So it is almost 1300 years before Pythagoras discovered the Pythagoras theorem. And this is the tablet what you’re seeing above.

The Pythagorean triplets are carved into three columns. So these are like three numbers which satisfy the Pythagoras rule. And these combinations of numbers are very crucial and they have a lot of applications. You can search for yourself.

Another ancient source of the Pythagoras triplets comes from Egypt. A mathematical document called Rhyn Papyrus, which is a mathematical worksheet of the ancient Egyptians. Apparently, it also has the Pythagorean triplets calculated. And this is almost dated to approximately 1500 BCE. And as you know, Egyptians are very famous for their triangular structures.

Finally from the Greeks, in 500 BCE, Pythagoras is the one who generalized the property of a right angle that the base square plus side square is equal to hypotenuse square. However, the Pythagoras theorem what we know today is given to us by Euclid, a Greek mathematician 200 years later after Pythagoras. He’s the one who has documented.

And that’s the manuscript what you’re seeing here. It is possibly a copy of Euclid’s original or could be a recopy of a Latin version. But nonetheless, it’s a manuscript explaining about the Pythagoras theorem.

Now, if we take a macro look, it is Babylonians in the 1800 BCE, Egyptians in the 1500 BCE, and Greeks in approximately 300 to 500 BCE, and Maharshi Bhaudhayana, who is again conservatively placed at 800 BC, gave the formula much before it is generalized by Pythagoras. It is not just about the antiquity, but also about the continuity.

Since many many thousands of years, the Sulba Sutras have been defining the way a Yagnyam needs to be organized. And till today, it is in practice. Such is the rich heritage, when it comes to Vedic geometry.

Yet, there is a high probability that most of you would have never heard of it. I just took this one as an example, so that most of us can connect and understand. But like this, there are Bhaudhayana, Apastamba, Manava, Katyaayana, Sulba Sutras, talking about the geometrical principles.

So that’s about the geometrical principles in Kalpa. And now let’s move on to Jyotishya.

Jyotishya Misunderstandings, misconceptions, pseudoscience, what not. It is totally entangled in a lot of preconceived notions. And allow me to set the record straight here.

There is Astrology, which deals mostly with the cultural element of predicting the future. And there is Astronomy, which is the study of the celestial bodies.

Now getting straight to the point, is Astrology or that future prediction business, is that scientific or not? Well the answer is, I don’t know. And I am not bothered either.

Let us take a worst case assumption that it is totally a pseudoscience. But the fact of the matter is, because of Astrology, Astronomy existed in India. Historically there have been a belief that the planetary positions impact people’s lives.

Now again I repeat, we are not at all discussing about that aspect here. And we are least interested about that. What we are rather interested is, in order to compute the planetary positions,

Jyotishya gave birth to incredible fields of mathematics. And this is not a joke or I am just trying to brew a conspiracy here. If at all there is any branch of knowledge that is highly misused and highly misunderstood, then it is Jyotishya.

Misused because of one set of people who commercialized this entire Jyotishya Shastra. And misunderstood because of another set of people who don’t know a thing about it, but just outright say that it is a pseudoscience.

Now let’s forget about these two highly polarized versions. Let’s try to find out what is in the middle with respect to geometry and at large with mathematics.

Time computation. It is the heart and soul of Jyotishya. Calculating the planetary positions to the minute is of top notch importance. And to do so, the ancient Indian astronomers and mathematicians developed a fleet of mathematical concepts in these three areas of geometry, trigonometry and calculus.

Let me put all these four blocks in a simple perspective. The time computation is of the top notch importance and in order to do that, the rate of change of planetary motion is also an integral part of it. And because of that calculus originated. And as a precursor to calculus, to calculate the ratio of observations of different planets, trigonometry as well took birth. And in order to construct the astronomical equipments, geometry as well thrived as part of Jyotishya. These three topics are very much intertwined with each other and it is difficult to explain one and leave the rest out.

I am not saying Indians founded all these branches of mathematics. I am saying there are significant contributions that came in from India for each of these fields which many of the people are not aware. Hope I am clear now.

Ujjain Mahakaal The Historical Powerhouse of Jyotishya Shastra

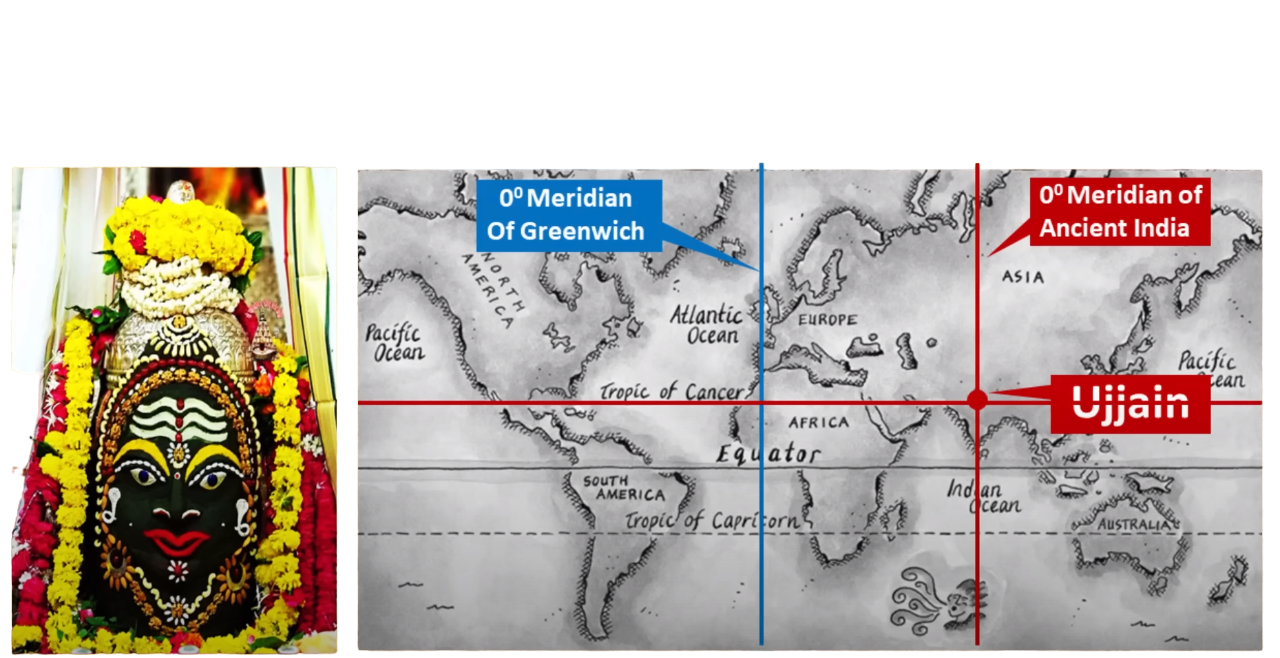
Speaking of Jyotishya, in India, Ujjain holds the top most importance for two main reasons. Number one, it is positioned right on the Tropic of Cancer and for many many centuries, the prime meridian of India used to cut through Ujjain as you are seeing it here. So counting of the day starts from Ujjain as per ancient Indian traditions.

However, the British after the colonization in 1884, they kind of consolidated all the meridians across the world where people are having their own prime meridians and moved it to Greenwich. Otherwise, historically, Ujjain is the place where time computation of the day starts.

Second thing, historically, Ujjain produced a lot of astronomers and mathematicians who contributed greatly to Indian mathematics. And here, Lord Shiva is worshipped as Mahakaal which means the lord of time and death.

Geometry in Jothishya

Coming to geometry in Jyotishya, where all it played its part, here is it as follows. It is used in construction of these astronomical observatories what you are seeing. A different kinds of structures for different purposes which we have in places like Jaipur and Ujjain.

The next, it also played its part in calculating the radiuses of different planets and also its role in trigonometrical observations to calculate the relative positions of the planets. And also in construction of certain astronomical equipments like astrolabes which are very indigenous to India. So we will just see very few interesting topics related to geometry and move on.

As part of Jyotishya, there are many Indian astronomers like Aryabhatta, Varahamihra, or Brahmagupta who gave incredible contributions towards it. Here is just one example from Aryabhattya given by Aryabhatta in 500 CE. He gave a formula for calculating the area of a circle without using pi.

Today, without pi we can’t imagine calculating the area of a circle. It’s going to be very very hectic. Not impossible but very hectic. But back then, like I said, there has been a tradition of measuring things using a rope in India.

समपरिणाहस्यार्धे विष्कम्भार्धहतमेव वृत्तफलम् _{– 7th Slokam, Ganithapada, Aryabhattiya}

So with that concept in mind, this formula is easily applicable, what Aryabhatta gave. Aryabhatta says that the area of a circle is half of the circumference multiplied by the radius. Circumference is something that you can measure with a rope and the radius as well. So using these the area of a circle can be calculated very easily without touching the value of pi. Because pi back then was still in a development mode.

You might not get an accurate result if you incorporate pi in your equations. And when you are talking about astronomical calculations even the fourth or fifth place of pi has huge impact.

Aryabhatta himself gave a better value for pi but at that time, the value given by the Chinese was far more accurate than the one which was given by Indians.

Talking about geometry and Jyotisha together, the most incredible contribution that came from India was in the year 1200 from Madhava. People were struggling to find the value of pi, an accurate one, adding up one decimal after other. So the development right from the discovery of the days when Greeks first identified that yes, there is a constant like pi, which is a ratio of the circumference to the diameter that can be used in the calculations.

The value of pi has been quite irrational. So Madhava is the first one to give the value of pi as an infinite series. That means it’s up to your patience. You can calculate as much as you want. This is no exaggeration but this invention is almost as good as landing man on Mars.

If it’s tough for you to believe, read the history of the pi and its evolution and you’ll get to know. So Madhava gave the value of pi in this small samskritam slokam. So he says that according to this samskritam slokam, this is what we get.

Infinite Series of Pi

व्यासे वारिधिनिहते रूपहृते व्याससागराभिहते। त्रिशरादिविषमसङ्ख्याभक्तमृणं स्वं पृथक् क्रमात् कुर्यात् ॥ _{Madhava – Gregory Series Gottfried Leibniz 17th Century CE}

The value of pi is equal to 4 multiplied by an alternating series of 1 minus 1 by 3 plus 1 by 5 minus 1 by 7 and so on till infinite.

In fact, he is the first one to express a finite quantity like pi in an infinite series. This is one of the fundamental stepping stones of calculus, integration by parts. And this is why I said calculus also has its roots in Jyotishya. But unfortunately we cannot discuss all that now. Maybe for some other day.

This series of pi is called as Madhava-Gregory series, which was initially invented by Madhava in the 14th century and reinvented by Gottfried Leibniz in 17th century. So in his honour, the series is named after Madhava as well as Gregory, saying that Madhava-Gregory series. Again, a vast majority of us are not aware of this, for obvious reasons.

Up next is geometry in Shilpa Shastra. Temples, the epicentre of Indian art, culture and heritage. So beautiful are the carvings. And the sculptures. But what’s actually behind them? Let’s quickly have a look.

Shilpa Shastra – Walls of Temples

Unlike Jyotishya Shastra and Kalpa, the geometrical concepts of Shilpa Shastra is not really something that we could possibly use or try to understand. It is so intricate and blended with the way the sculptings are done. So here you see as an example, the walls of a temple, there are different varieties of designs depending on the deity of the temple.

There are specified designs, not just any random ones, to be carved in accordance with the scriptures of Agama, Manasara or Shilpa. These are different books which describe how a temple construction needs to be done.

Shilpa Shastra – Pillars of Temples

Shilpa Shastra also gives the geometrical guidelines about constructing and carving different kinds of pillars as you see here. It gives the structural guidelines as well as the aesthetic guidelines in building the pillars and other parts of the temple. \

Shilpa Shastra – Arches

Here are some blueprints about the arches that would be constructed in the temple. The interesting part is, all these designs are explained in form of Samskritam slokams. It is quite interesting to see how such great details are encoded in Samskritam.

Shilpa Shastra – Vimanas

Here are the most catchy parts of the temple, the Vimanas or the Gopuram. Shilpa Shastra explains great detail about how these need to be layered and sculpted both for its structure as well as for its aesthetics. And in all, geometrical principles are well blended in each of them.

There we have the last category, Srividya, which also has complex geometrical procedures blended into it. Srividya is a path of devotion in which Sri Lalita Parameswari is worshipped as the epitome of the nature and the cosmos. As part of this practice, what you are seeing on the picture are called as yantras. These yantras are manifestations of the gods themselves.

So that’s what the practice is all about. People meditate on these yantras as part of their spiritual process. But as we are looking from a geometry standpoint, we will see it from that angle.

To understand these geometrical diagrams called yantras, basically they are revered as a layout in which each vertex, line, corner holds a deity and it’s like a labyrinth where people start meditating through their paths, navigating towards the centre of the yantra.

It’s a bit complicated and I myself don’t have a clear cut understanding about the spiritual aspects of it. So let’s limit ourselves from the geometry standpoint. The most important topic here is, as you see, we have a lot of deities in each and every space of this diagram.

So that translates to incredible precision in the geometrical structures which are the yantras. So to create these geometrical structures or the yantras, a lot of techniques have originated in building these diagrams. And this is a very very ancient culture in there are many temples where you have these yantras carved into either the floor or the ceiling or other parts of the temples.

Here is a manuscript detailing out some yantra and describing the way one has to follow it. It’s just a snippet from a very ancient manuscript. You see here the diagrams, how they are drawn. These diagrams represent a specific deity which one chooses to worship in his or her path of devotion.

Ganesh Yantram

So here is a specific example of Ganesha yantra which is a manifestation of Lord Ganesha himself. So that’s what and how it is revered. And this is just a rough sketch but when it comes to actually consecrating such kind of a yantra, a high geometric precision is ensured. And as part of it, there are a lot of construction techniques as part of the Vedic geometry that designs these yantras.

Bhairava Yantram

This one is a Bhairava yantra, manifestation of Lord Shiva in the form of Bhairava. One of the most ferocious forms of Lord Shiva. And this yantra is Mahakali yantra, which is a manifestation of Kalima. These look like a simple diagrams but the proportions and precession and the symmetricity, they matter a lot when it comes to consecrating them.

Sri Mahalakshmi and Sri Yantram

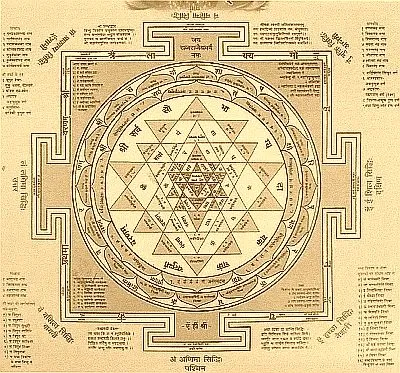
This one is Sri Mahalakshmi yantra, again a manifestation of Goddess Sri Mahalakshmi. And of all the yantras, Sri yantra is revered as the most important yantra when it comes to Srividya. And it’s a highly complex geometrical structure where the precision matters to the pixel.

It has nine triangles which shows as a confluence of Shiva and Shakti holding the top most importance in the spiritual process. There is a lot of mathematical analysis that was done in many universities across India, Europe and US on Sri Chakra and its symmetricity and other geometrical properties.

At this point in time, I don’t fully understand it. And the day I understand, we’ll definitely do a detailed documentary about it.

Well now, that’s a very brief overview about Vedic geometry and how it pans across all these four areas. I’d like to come back to Sulbha Sutras again. I was really surprised to learn the fact that it is the world’s oldest applied geometry that is still running in the tradition till today.

Broadly, a very derogatory term called mythology is often attributed to anything that you talk about ancient Indian history. Well, that’s not true. There are many, many mathematical or scientific concepts like Sulbha Sutras. I do agree that there are certain pseudo-scientific topics as well.

That’s a very small portion of it. But largely, the history of India has always been tightly coupled with both science and devotion together. And Vedic geometry is an example of scientific heritage of India.